Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input kedalam suatu ruang output. Fuzzy secara bahasa diartikan sebagai kabur atau samar-samar. Suatu nilaidapat bernilai besar atau salah secara bersamaan. Dalam fuzzy dikenal derajat keanggotaan yang memiliki rentang nilai 0 (nol) hingga 1(satu). Berbeda dengan himpunan tegas yang memiliki nilai 1 atau 0 (ya atau tidak). Logika Fuzzy merupakan seuatu logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar atau salah. Dalam teori logika fuzzy suatu nilai bias bernilai benar atau salah secara bersama. Namun berapa besar keberadaan dan kesalahan suatu tergantung pada bobot keanggotaan yang dimilikinya. Logika fuzzy memiliki derajat keanggotaan dalam rentang 0 hingga 1. Berbeda dengan logika digital yang hanya memiliki dua nilai 1 atau 0. Logika fuzzy digunakan untuk menterjemahkan suatu besaran yang diekspresikan menggunakan bahasa (linguistic), misalkan besaran kecepatan laju kendaraan yang diekspresikan dengan pelan, agak cepat, cepat, dan sangat cepat. Dan logika fuzzy menunjukan sejauh mana suatu nilai itu benar dan sejauh mana suatu nilai itu salah. Tidak seperti logika klasik (scrisp)/ tegas, suatu nilai hanya mempunyai 2 kemungkinan yaitu merupakan suatu anggota himpunan atau tidak. Derajat keanggotaan 0 (nol) artinya nilai bukan merupakan anggota himpunan dan 1 (satu) berarti nilai tersebut adalah anggota himpunan. Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input kedalam suatu ruang output, mempunyai nilai kontinyu. Fuzzy dinyatakan dalam derajat dari suatu keanggotaan dan derajat dari kebenaran. Oleh sebab itu sesuatu dapat dikatakan sebagian benar dan sebagian salah pada waktu yang sama (Kusumadewi. 2004) Logika Fuzzy memungkinkan nilai keanggotaan antara 0 dan 1, tingkat keabuan dan juga hitam dan putih, dan dalam bentuk linguistik, konsep tidak pasti seperti "sedikit", "lumayan" dan "sangat" (Zadeh 1965).
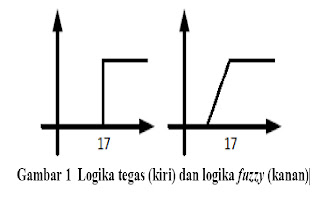
Misalnya dalam kehidupan sehari-hari, dewasa didefinisikan dengan berusia 17 tahun ke atas. Jika menggunakan logika tegas, seseorang yang berusia 17 tahun kurang 1 hari akan didefinisikan sebagai tidak dewasa. Namun dalam logika fuzzy, orang tersebut dapat dinyatakan dengan hampir dewasa.
Salah satu contoh pemetaan suatu input-output dalam bentuk grafis seperti terlihat di bawah ini:
Persediaan barang akhir Persediaan barang akhir Persediaan barang esok Persediaan barang esok Kotak Hitam Ruang Input (semua total persediaan barang yang mungkin) Ruangutput( semuaj umlah produksi barang yang mungkin) Pemetaan Input-output pada masalah produksi Diberikan data persediaan barang, berapa jumlah barang yang harus diproduksi?
Alasan Digunakannya Logika Fuzzy
Ada beberapa alasan mengapa orang menggunakan logika fuzzy, antara lain :
1.Konsep logika fuzzy mudah dimengerti. Konsep matematis yang mendasari penalaran fuzzy sangat sederhana dan mudah dimengerti
2.Logika fuzzy sangat fleksibel
3.Logika fuzzy memiliki toleransi terhadap data-data yang tidak tepat
4.Logika fuzzy mampu memodelkan fungsi-fungsi nonlinear yang sangat kompleks
5.Logikafuzzy dapatmembangundanmengaplikasikanpengalaman-pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan
6.Logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara konvensional.
7.Logika fuzzy didasarkan pada bahasa alami
himpunan dan fungsi keanggotaan fuzzy
Himpunan Fuzzy
Himpunan Fuzzy Merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variable fuzzy.
Himpunan fuzzy adalah pengelompokan sesuatu berdasarkan variabel bahasa (linguistik variable), yang dinyatakan dengan fungsi keanggotaan, dalam semesta U. Keanggotaan suatu nilai pada himpunan dinyatakan dengan derajat keanggotaan yang nilainya antara 0.0 sampai 1.0
Himpunan fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian hingga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Nilai keanggotaannya menunjukkan bahwa suatu item tidak hanya bernilai benar atau salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar
Pada himpunan tegas(crisp), nilai keanggotan suatu item x dalam suatu himpunan A yang sering ditulis dengan μA[x], memiliki 2 kemungkinan yaitu:
•Satu(1), yang berarti bahwa suatu item menjadi anggota dalam suatu himpunan, atau
•Nol(0), yang berarti bahwa suatu item tidak menjadi anggota dalam suatu himpunan
)
•Contoh1:
Jikadiketahui:
S = [1, 2, 3, 4, 5, 6] adalah semesta pembicaraan
A = [1, 2, 3]
B = [3, 4, 5]
Maka dapat dikatakan:
��Nilai keanggotaan 2 pada himpunan A, μA[2] = 1, karena 2 єA
��Nilaikeanggotaan4 pada himpunan A, μA[4] = 0, karena 4 ∉ A
•Contoh2 :
Misalkan variable umur dibagi 3 kategori, yaitu:
MUDA umur< 35 tahun
PAROBAYA 35 ≤umur≤55thn
TUA umur> 55 tahun
Maka dengan himpunan crisp disimpulkan:
•Apabila seseorang tidak berusia 34 tahun, maka ia dikatakan MUDA (μ MUDA [34] = 1)
•Apabila seseorang berusia 35 tahun, maka ia dikatakan TIDAK MUDA (μ MUDA [35] = 0)
Jika pada himpunan crisp, nilai keanggotaan hanya ada 2 kemungkinan yaitu 0 dan 1, maka pada himpunan fuzzy nilai keanggotaan terletak pada rentang 0 sampai1.
Himpunan crisp untuk menyatakan umur bias tidak adil karena adanya perubahan kecil saja pada suatu nilai mengakibatkan perbedaan kategori yang cukup signifikan.
)
•Himpunan fuzzy memiliki 2 atribut:
a.Linguistik, yaitu penamaan suatu grupy ang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, seperti: MUDA, PAROBAYA, TUA
b.Numeris, yaitu suatu nilai(angka) yang menunjukan ukuran dari suatu variable seperti: 40, 25, 35
)
•Hal-hal yang terdapat pada system fuzzy :
a.Variabel Fuzzy, merupakan variable yang hendak dibahas dalam suatu system fuzzy, seperti umur, temperatur, dsb
b.HimpunanFuzzy, merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variable fuzzy
Contoh:
Variabel umur: MUDA, PAROBAYA, TUA
Variabel suhu: DINGIN, SEJUK, NORMAL, PANAS, HANGAT
c.Semesta Pembicaraan (SP), adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variable fuzzy.
SP merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan.
NilaiSP dapat berupa bilangan positif atau pun negatif.
Adakalanya nilai SP tidak dibatasi batas atasnya.
Contoh:
- SP untuk variable umur: [0, +∞)
- SP untukvariabe lsuhu: [0, 40]
d.Domain, adalah keseluruhan nilai yang diijinkan dalam semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Dapatberupabilanganpositifataunegatif
Contoh domain himpunan fuzzy :
MUDA= [ 0 45]
PAROBAYA= [ 35 55]
TUA= [ 45 +∞]
DINGIN= [ 0 20]
SEJUK= [ 15 25]
NORMAL= [ 20 30]
HANGAT= [ 25 35]
PANAS= [ 30 40]
FUNGSI KEANGGOTAAN fuzzy
Fungsi keanggotaan fuzzy adalah suatu kurva yang menunjukan pemetaan titik-titik input data ke dalam nilai keanggotaannya (derajat keanggotaan) yang memiliki interval antara 0 sampai1. Dalam logika tegas, fungsi keanggotaan menyatakan keanggotaan pada suatu himpunan. Fungsi keanggotaan χA(x) bernilai 1 jika x anggota himpunan A, dan bernilai 0 jika x bukan anggota himpunan A. Jadi, fungsi keanggotaan ini hanya bisa bernilai 0 atau 1.
χA : x à {0,1}
Sedangkan dalam logika fuzzy, fungsi keanggotaan menyatakan derajat keanggotaan pada suatu himpunan. Nilai dari fungsi keanggotaan ini berada dalam selang [0,1], dan dinyatakan dengan μA.
Fungsi keanggotaan μA(x) bernilai 1 jika x anggota penuh himpunan A, dan bernilai 0 jika x bukan anggota himpunan A. Sedangkan jika derajat keanggotaan berada dalam selang (0,1), misalnya μA(x) = μ, menyatakan x sebagian anggota himpunan A dengan derajat keanggotaan sebesar μ.
•Ada beberapa fungsi yang biasa digunakan :
a.Representasi Linear
Ada 2 kemungkinan himpunan fuzzy linear yaitu
1.Kenaikan himpunan dimulai pada nilai domain yang memiliki derajat keanggotaan nol[0] bergerak ke kanan menuju nilai domain yang memiliki derajat keanggotaan lebih tinggi RepresentasiLinear Naik
FungsiKeanggotaan:0;x ≤aμ[x] = (x-a)/(b–a) ; a ≤x ≤b1;x ≥b
)
2.Garis lurus dimulai dari nilai domain dengan derajat keanggotaa ntertinggi pada sisi kiri, kemudianbergerakmenurunkenilaidomain yang memiliki derajat keanggotaan lebih rendah RepresentasiL inear TurunFungsiKeanggotaan:(x-a)/(b–a) ;a ≤x ≤bμ[x] = 0;x ≥b
)
b. Representasi Kurva Segitiga
c. Representasi Kurva Trapesium
d.Representasi Kurva bentuk Bahu
e.Representasi Kurva-S
f.Representasi Kurva Bentuk Lonceng, ada3 jenis, KurvaPI, KurvaBeta danKurvaGAUSS
g.Koordinat Keanggotaan
Operator Dasar Zadeh
Operator Dasar Zadeh
•Operator AND
Operator ini berhubungan dengan operasi interseksi padah impunan. α-predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan
μA∩B = min(μA[x], μB[y])
Operator OR
Operator ini berhubungan dengan operasi union pada himpunan α-predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan
μAUB = max(μA[x], μB[y])
•Operator NOT
Operator ini berhubungan dengan operas ikomplemen himpunan. α-predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan
PENALARAN MONOTON
PENALARAN MONOTON
Metode ini digunakan sebagai dasar untuk teknik implikasi fuzzy. Jika 2 daerah fuzzy direalisasikan dengan implikasi sederhana sebagai berikut:
IF x is A THEN y is B
transfer fungsi:
Y = f ((x, A), B)
Maka system fuzzy dapat berjalan tanpa harus melalui komposisi dan dekomposisi fuzzy. Nilai output dapat diestimasi secara langsung dari nilai keanggotaan yang berhubungan dengan antesedennya.
Pada tahapan ini sistem menalar nilai masukan untuk menentukan nilai keluaran sebagai bentuk pengambil keputusan. Sistem terdiri dari beberapa aturan, maka kesimpulan diperoleh dari kumpulan dan korelasi antar aturan. Ada 3 metode yang digunakan dalam melakukan inferensi sistem fuzzy, yaitu max, additive dan probabilistik OR. metode max, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikanya ke output dengan menggunakan operator OR (union). Secara umum dapat ditulis[4]
μdf (xi) max (μdf(xi,) μkf(xi)) (13)
Selain itu, salah satu model penalaran yang banyak digunakan adalah max-min. Dalam penalaran ini, pertama-tama dilakukan proses operasi min sinyal keluaran lapisan fuzzyfikasi, kemudian diteriskna dengan operasi max untuk mencari nilai keluaran yang selanjutnya akan didefuzzyfikasikan sebagai bentuk keluaran pengendali [2]. Operasi max-min tersebut dapat dinyatakan sebagai berikut.
Operasi min atau irisan
(14) baifbbaifababa),min(
Operasi max atau gabungan
(15) baifbbaifababa),max(
FUNGSI IMPLIKASI
Kaidah fuzzy If-Then (dikenal juga sebagai kaidah fuzzy, implikasi fuzzy atau pernyataan kondisi fuzzy) diasumsikan berbentuk:
Bentuk umum aturan yang digunakan dalam fungsi implikasi:
IF x is A THEN y is B
Dengan x dan y adalah skalar, A dan B adalah himpunan fuzzy. Proposisi yang mengikuti IF disebut anteseden, sedangkan proposisi yang mengikuti THEN disebut konsekuen.
•Secara umum, ada dua fungsi implikasi, yaitu:
1.Min (minimum), fungsi ini akan memotong output himpunan fuzzy
2.Dot (product), fungsi ini akan menskala output himpunan fuzzy
SISTEM INFERENSI FUZZY
Sistem kendali logika fuzzy disebut juga sistem Inferensi Fuzzy (Fuzzy Inference System/FIS) atau fuzzy inference engine adalah sistem yang dapat melakukan penalaran dengan prinsip serupa seperti manusia melakukan penalaran dengan nalurinya.
Terdapat beberapa jenis FIS yang dikenal yaitu Mamdani, Sugeno dan Tsukamoto. FIS yang paling mudah dimengerti, karena paling sesuai dengan naluri manusia adalah FIS Mamdani. FIS tersebut bekerja berdasarkan kaidah-kaidah linguistik dan memiliki algoritma fuzzy yang menyediakan sebuah aproksimasi untuk dimasuki analisa matematik.
MetodeTsukamoto
Setiap konsekuen pada aturan yang berbentuk IF-THEN harus direpresentasikan dengan suatu himpunan fuzzy dengan fungsi keanggotaan yang monoton. Sebagai hasilnya, output hasil inferensi dari tiap-tiap aturan diberikan secara tegas berdasarkan α-predikat. Hasil akhirnya diperoleh dengan menggunakanr ata-rata terbobot
MetodeMamdani
Sering dikenal dengan nama Metode Max-Min. Metode ini diperkenalkan oleh Ebrahim Mamdani pada tahun1975. Untuk mendapatkan output diperlukan 4 tahapan:
1.Pembentukanhimpunanfuzzy
Variabelinput maupun output dibagi menjadi satu atau lebih himpunan
2.Aplikasi fungsi implikasi
Fungsi implikasi yang digunakan adalah Min
3.Komposisiaturan
Ada tiga metode yang digunakan dalam melakukan inferensi system fuzzy :
a.Metode Max
b.Metode Additive (SUM)
c.Metode ProbabilistikOR
4.Penegasan (defuzzy)
Input dari de fuzzi fikasi adalah suatu himpunan yang diperoleh dari komposisi aturan-aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu bilangan pada domain himpunanfuzzy tersebut.
•Beberapa metode defuzzifi-kasiaturan MAMDANI :
a.Metode Centroid (Composite Moment)
b.Metode Bisektor
c.Metode Mean of Maximun (MOM)
d.Metode Largest of Maximum (LOM)
e.Metode Smallest of Maximum (SOM)
Metode Sugeno
Penalaran ini hamper sama dengan penalaran Mamdani, hanya sajaoutput (konsekuen) system tidak berupa himpunan fuzzy, melainkan berupa konstanta atau persamaan linear.
a.Model Fuzzy Sugeno Orde-Nol
Bentuk Umum:
IF (X1 is A1) ��(X2is A2) ��(X3is A3) ��…. ��( XNisAN) THEN z = k
Dengan Ai adalah himpunan fuzzy ke-I sebagai anteseden, dan k adalah konstanta (tegas) sebagai konsekuen
Model Fuzzy Sugeno Orde-Satu
Bentuk Umum:
IF (X1 is A1) ��….��(XNisAN) THEN z = p1* x1 + …+ pN* XN + q
denganAi adalahhimpunanfuzzy ke-I sebagai anteseden, dan pi adalah suatu konstanta ke-I dan q merupakan konstanta dalam konsekue
data base fuzzy
Sebagian besar basis data standar diklasifikasikan berdasarkan bagaimana data tersebut dipandang oleh user dan menggunakan query untuk mencari data yang diinginkan. Namun terkadang dibutuhkan suatu data yang bersifat ambiguous, maka digunakan basis data fuzzy. Salah satu diantaranya adalah model Tahani. Basis data fuzzy model Tahani masih tetap menggunakan relasi standar, hanya aja model ini menggunakan teori himpunan fuzzy untuk mendapatkan informasi pada query-nya.
KESIMPULAN
Makalah harus memiliki suatu kesimpulan. Sama seperti makalah ini, kita bisa mengambil beberapa kesimpulan. Kesimpulan-kesimpulan tersebut antara lain:
1. Logika fuzzy adalah logika yang mengandung unsur ketidakpastian.
2. Keanggotaan dalam himpunan fuzzy dinyatakan dengan derajat keanggotaan. Suatu nilai dapat menjadi anggota dua himpunan sekaligus dengan derajat yang berbeda.
3. Kendali logika fuzzy dilakukan dengan proses fuzzyfikasi, penalaran sesuai dengan aturan, dan defuzzyfikasi.
4. Sistem kendali logika fuzzy cukup praktis diaplikasikan dalam berbagai bidang.











2 komentar:
Kita juga mempunyai jurnal mengenai Logika Fuzzy, silahkan dihubungi dan dibaca. Berikut linknya:
http://repository.gunadarma.ac.id/bitstream/123456789/2654/1/Kommit2000_Elektro_010.pdf
Semoga bermanfaat!
saya mau tanya perbedaan antara fuzzy tsukamoto dan mamdani itu bagaimana?
saya masih kurang paham tentang itu
terimakasih
Posting Komentar